The determination of reserves is a fundamental calculation in reservoir engineering. The material balance method uses actual reservoir performance data, and therefore is generally accepted as the most accurate procedure for estimating original hydrocarbons-in-place. In order to generate a traditional material balance plot, the well is shut in at several points during its producing life to obtain the average reservoir pressure. However, this is sometimes impractical, and usually the duration of the shut-in is often not long enough to obtain an accurate measurement. A FMB uses the concept of boundary-dominated flow or pseudo-steady state flow, as well as flowing pressures and rates, to calculate original hydrocarbons-in-place.
Pseudo-steady state
The flow of hydrocarbons through a porous medium can be divided into transient and boundary-dominated flow periods. When a well has reached boundary-dominated flow, its behavior is governed by the pseudo-steady state equations. When a reservoir is in pseudo-steady state flow and the flow rate is constant, the pressure at all locations in the reservoir declines at the same rate. The figure below depicts pressures in the reservoir at all locations when the wellbore is located at the left, and the exterior boundary of the reservoir is located at the right. Each of the lines, one, two, and three, represents the pseudo-steady state pressure in the reservoir when the well is flowing at a constant rate. The pressure decline from "time one" to "time two" is the same throughout the reservoir as the curves are parallel.

The traditional material balance method shuts in the well several times during the productive life of the reservoir, and lets the pressure stabilize to an average pressure p1. Similarly, the pressure profile in the reservoir at later times would result in shut-in average reservoir pressures of p2 and p3. It is evident that the drop in pressure from p1 to p2 to p3 is the same as the drop in pressure at any selected point along curves one, two, or three. A convenient point for analysis could be at the wellbore. Remembering that curves one, two, and three represent a flowing well, it is evident that a plot of the flowing wellbore pressure (pwf1, pwf2, pwf3) should be parallel to a plot of the average reservoir pressure (p1, p2, p3).
In a flowing situation, the average reservoir pressure clearly cannot be measured. However, as demonstrated above, in a stabilized-flow situation, there is very close connectivity between well-flowing pressures, which can be measured, and the average reservoir pressure. The pressure drop measured at the wellbore while the well is flowing at a constant rate is the same as the pressure drop that is observed anywhere in the reservoir, including the location that represents average reservoir pressure. This is only true if pseudo-steady state conditions are present, meaning that all boundaries have been reached, and the rate of withdrawal is constant for the period of time when pwf1 through pwf3 were measured.
Gas
For gas reserves, the material balance p/z plot is a very useful tool for estimating original gas-in-place (OGIP). The conventional p/z plot uses the extrapolated straight-line trend of measured shut-in pressures to predict OGIP. The same can be done with flowing pressures, provided that the pseudo-steady state assumption is valid (that is, constant rate boundary-dominated flow). For gas, the pseudo-steady state equation for a vertical well in the center of a circular reservoir is as follows:
Furthermore, the pressure decline illustration above shows that a material balance plot of flowing wellbore pressures should be parallel to the material balance plot using the average static reservoir pressure. This procedure, shown below, consists of a plot of pwf / Z, where pwf is the flowing sandface pressure at the wellbore vs. cumulative production. A straight line drawn through the flowing sandface pressure data and then extrapolated parallel from the initial reservoir pressure gives the OGIP.
Basically this means that the slope of the resulting best-fit line should be the same as the slope of the conventional p/z line, but shifted upwards, so that it falls through the initial p/z point. This is the flowing gas material balance. Therefore, using flowing pressures and rates, a material balance analysis can be conducted without shutting in the well.

This technique can use either flowing sandface pressures or flowing surface pressures. However, when using surface pressures, the line drawn parallel to the data must pass through the initial "wellhead" pressure, not the initial "reservoir" pressure.
Variable rate flowing p/Z**
Most gas wells do not have extended periods of constant-rate production. Thus the above concepts cannot be directly applied. A typical gas well may have a production profile as shown below.

With the above profile, we cannot assume a constant pressure difference between average reservoir conditions and flowing conditions. We know that during boundary-dominated flow:
where:
bpss represents the pressure loss due to the steady-state inflow of gas, and is assumed to be constant over time.
For a variable-rate system, the equation above clearly shows that the difference between reservoir p/z and flowing p/z is not constant, but rather is a function of flow rate. Since the flow rate is known, we need only to determine the value of bpss, using some independent method. Note that the value of bpss did not have to be explicitly determined for the constant rate case because the total value of "q bpss" (the product of flow rate and bpss) was determined graphically.
One way to obtain a reliable estimate of bpss is to plot the production and flowing-pressure data in the following manner:

The straight line portion of this graph represents boundary-dominated flow, and the y-intercept is bpss. This value of bpss may then be used in the above equation to calculate the average reservoir pressure. Note that the value of bpss is always subject to interpretation as it depends on proper identification of the stabilized (straight line) section of the above graph.
Alternatively, bpss can be obtained from the Agarwal-Gardner FMB analysis plot. As shown below, 1/bpss is the y-intercept on that plot. Obtaining the value from the best-fit straight line interpretation below, the flowing p/z** values can be calculated.

Agarwal-Gardner normalized rate
An alternative to the flowing p/z plot is the normalized rate / normalized cumulative analysis. The normalized rate approach applies to both oil and gas reservoirs, and works for constant, or variable-rate systems. Its advantage is its flexibility and ease of use. Its primary drawback is that the resulting analysis plot is not as intuitive as that of the flowing p/z.
The procedure is similar to the pseudo-steady state approach, but involves plotting the inverse of the pseudo-steady state equation, so that a declining trend is produced. The normalized rate is plotted against the normalized cumulative. A line is then drawn through the best-fit of the points, and the x-intercept is the OGIP. The governing equation for the straight-line equation for the Agarwal-Gardner analysis is:
where:
and:
To calculate the average reservoir pressures, use the general material balance equation below, and first assume a value for OGIP. This is an estimate and can be obtained from volumetrics, modeling, or some other analysis.
The step-by-step procedure for generating the Agarwal-Gardner analysis for a gas well with varying flow rate is:
1. Convert initial pressure to pseudo-pressure.
2. Convert all flowing pressures to pseudo-pressures.
3. Assume a value for OGIP.
4. Calculate p/z** from the general material balance equations.
5. Using lookup tables, find the corresponding average reservoir pressure.
6. Convert average reservoir pressure to pseudo-pressure.
7. Using the equations above, plot a graph of normalized rate versus normalized cumulative.
8. Draw a straight line through the best-fit of the data points. (The intercept on the x-axis gives OGIP.)
9. Using this new value for OGIP, repeat steps 4-8 until the OGIP converges.
Productivity index
The productivity index of a well is a measure of the production rate achievable under a given drawdown pressure, which is the difference between the average reservoir pressure and the flowing sandface pressure. Defined as the flow rate per unit pressure drop, the productivity index gives an indication of the production potential of a well.
From the pss equation above:
therefore:
From a reservoir point of view, well management primarily depends on the well productivity index, which is in turn dependent on rock and fluid properties. One of the principal causes for the reduction in well productivity is formation damage around the wellbore. For an FMB analysis, when the "correct" OGIP is found, the productivity index dataset should be relatively flat, indicating that the productivity index is not drastically changing over time.

As can be seen above, the productivity index equation is very similar to the traditionally used simplified absolute open flow (AOF) equation, shown below. The major differences being that:
- The productivity index is written rigorously using pseudo-pressures and the AOF equation uses the simpler pressure- squared method.
- The AOF equation introduces the concept of laminar / turbulent flow using the exponent "n".
Assuming n = 1:
Advanced gas material balance techniques – p/Z**
The graphical simplicity of the conventional p/Z material balance analysis makes it quite popular. Developed for a "volumetric" gas reservoir, it assumes a constant pore volume of gas, and accounts for the energy of gas expansion. However, advanced methods have been developed to account for other sources of energy, such as the effects of formation compressibility, residual fluids expansion, and aquifer support. Furthermore, these methods can also account for other sources of gas storage such as connected reservoirs, or adsorption in coal / shale. The FMB analysis accounts for all of these effects, if required. The formulation for the calculation of p/Z** is highlighted below:
where:
and total compressibility is defined as:
The table below outlines the formulations for the total-compressibility equations for all reservoir types.
| Definition | Comment |
|---|---|
|
|
Water-drive reservoir |
|
|
co, cw, and cf are constant cep is the approximate form |
|
|
co, cw, and cf are constant cep is the simple form |
|
|
co, cw, and cf are pressure-sensitive without matrix shrinkage. cep is the rigorous form |
|
|
co, cw, and cf are pressure-sensitive with matrix shrinkage. cep is the rigorous form |
|
|
Shale gas reservoir |
| Note: | For more information, see Moghadam et al. (2009). |
Oil
The basis for the FMB of oil comes from both the definition of compressibility and the steady-state inflow equation. Compressibility is defined as:
This equation shows that compressibility is defined as the relative change in fluid volume per unit change in pressure.

The above schematic demonstrates that as pressure is reduced, the fluid expands to occupy a larger volume such that V2 > V1. However, most reservoirs can reasonably be expected to have a constant pore volume such that PV1 = PV2. Consequently, as we produce fluid from a reservoir, the remaining fluid in the reservoir expands to fill the pore volume, and so the reservoir pressure is reduced.
Production from an undersaturated* oil reservoir can be visualized as follows:

* There is no free gas since the reservoir pressure is greater than the bubble-point pressure of the oil.
Thus, the change in pressure is the difference between the initial reservoir pressure and the average reservoir pressure, and the change in volume is the produced volume up to that point in time. Knowing that the initial volume is the total oil-in-place, these terms are applied to the compressibility equation.
Combining the above relationship with the pseudo-steady equation, and then rearranging and substituting for material balance time gives the following:
The above equation clearly illustrates the relationship between initial pressure, flowing pressure, and rate.

From the figure above, it is apparent that the pseudo-steady state equation is the sum of two distinct pressure-loss components:
Pressure loss due to depletion:
Pressure loss due to inflow:
The advantage of the pseudo-steady state formulation is that the average reservoir pressure is eliminated during the addition of pressure loss due to depletion and pressure loss due to inflow, and thus is not explicit in the equation. This is an obvious advantage because the average reservoir pressure is an unknown. Since both terms (pressure loss due to depletion and pressure loss due to inflow) are functions of rate, we can simplify the pseudo-steady state equation as follows:
where:
A graph of normalized pressure vs. time produces a straight line, the slope of which provides the original oil-in-place (OOIP). This is the most basic form of FMB, and is directly applicable to undersaturated oil reservoirs. In well testing, this procedure is commonly referred to as a "reservoir limits test".

However, to make it more intuitive and similar to a gas material balance plot, the pseudo-steady state equation above is rearranged to the following:
Plotting normalized rate vs. normalized cumulative (similar to the Agarwal-Gardner plot), the following plot is derived, where the x-intercept is equal to the OOIP.

The above equation and associated figure describe the flowing oil material balance analysis for a volumetric circular reservoir.
Static pressure data
If static pressures are available, you can use this data as an independent confirmation of the OOIP. This is an equation describing material balance for an oil reservoir for a simple case (that is, no gas cap, no water production), assuming constant total compressibility:

This equation can be rearranged as:

Therefore, plotting average pressure against
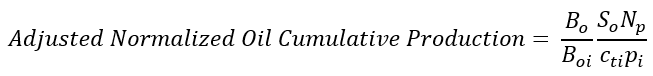
should follow a straight line, with the x-intercept of the line being equal to the OOIP.
Accounting for variation in oil properties
The derivation for oil Flowing Material Balance (FMB) given above is valid under the assumption that the variation of oil and rock properties (ct, Bo, μo, and k) with pressure is negligible. That assumption is valid for some cases, but sometimes (for example, for oil with high gas content, or for cases with pressure-dependent rock properties), it is important to accurately account for variations in oil and rock properties.
This is done similarly to Agarwal-Gardner FMB analysis for gas.
Oil pseudo-pressure is defined as:
Total pseudo-pressure drop can then be written in terms of oil pseudo-pressure and can be presented as:
Under conditions of pseudo-steady state, the pressure drop due to Darcy flow and flow rate are related by:
Where Constant is defined by reservoir and completion geometry, but does not change with pressure. Using rules of integration, this can be re-arranged as:
Therefore, pressure drop due to Darcy flow in terms of oil pseudo-pressure can be expressed as:
Where b'pss does not vary with pressure.
Using this formulation for pressure drop due to Darcy flow, total pressure drop can be presented as:
Dividing both sides by Δppo b'pss and re-arranging we get:
(Note that we added N to both the numerator and denominator of the last term.)
This equation is used to create a plot for oil FMB analysis that accounts for variation of oil and formation properties.
The y-values for each data point can be readily calculated based on production data:
To calculate x-values, use an iterative procedure:
1. Estimate a value for oil in place, Nguess.
2. Calculate the average reservoir pressure based on Nguess, known production data, and using rigorous material-balance calculations.
3. Calculate x-values:
4. Generate an FMB plot (y-values vs. x-values).
5. Draw a straight line through the data points corresponding to boundary-dominated flow (the late portion of the data).
6. The y-intercept of the line equals 1/b'pss, and the slope of the line equals 1/(Nb'pss); therefore N can be calculated.
7. Compare the calculated N with Nguess. If they are not equal, set the next Nguess to the value calculated in step 6, and return to step 1.
8. Iterate until N = Nguess.
This approach is described by Stalgorova and Mattar (2016).