Changing wellbore storage occurs when one of the following conditions exists within the wellbore:
- Changing wellbore fluid compressibility
- Phase redistribution
- Change in the type of storage from a changing liquid level to a liquid filled wellbore
The phenomenon of phase redistribution occurs in a well which is shut in at the surface with gas and liquid flowing simultaneously into the tubing. In these situations, the gravity effects cause the liquid to fall and the gas to rise to the surface. Because of the very low compressibility of liquid and no extra room for gas to expand in a closed chamber, the re-distribution of phases causes a net increase in the wellbore pressure. When the phenomenon is present in a buildup test, the extra pressure surge in the wellbore is relieved through the formation. Eventually, equilibrium will be attained between the wellbore pressure and the formation pressure adjacent to the wellbore. However, at early times, the wellbore pressure may exceed the formation pressure causing an anomalous hump in the buildup pressure which cannot be analyzed in a conventional way with only the dimensionless wellbore storage constant (CD). In order to deal with phase re-distribution, two models have been proposed by Fair (1981) and Hegeman et al. (1993) which introduce two additional dimensionless wellbore constants: apparent storage (CaD) and the pressure parameter (CpD).
Fair considered the exponential expression for the dimensionless anomalous pressure (ppD) rise as:
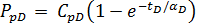
Later, Hegeman et al. showed that the negative CpD values in the Fair model can be used for buildup data that has an anomalous pressure decrease. Therefore, for these wells, they argued that using an error function to model the anomalous pressure may allow for better modeling of field data with increasing or decreasing storage. Thus, Hegeman et al. proposed that:
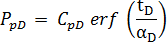
However, it has been found in practice that the models of Fair and Hegeman et al. are not substantially different.
The following plots illustrate the effects of the three dimensionless storage parameters on the dimensionless typecurves.
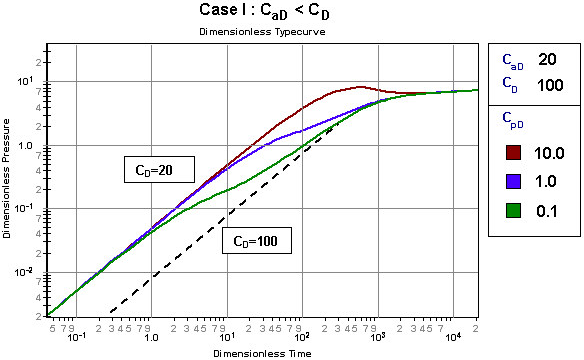
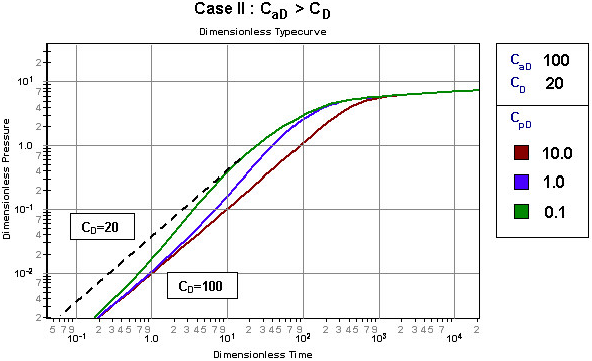
Dimensionless wellbore storage constant (CD)
The wellbore storage constant in dimensionless form is defined as:
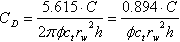
A large value of dimensionless wellbore storage is associated with a large wellbore volume (Vw). In practice, a range of values from 500 to 10000 has been observed. Occasionally, a value much greater than 10,000 is observed when actual test data are matched against a typecurve. In such cases, it is considered that some part of the formation (high permeability or fracture) is in communication with the wellbore, and is acting as an extension to it.
In a horizontal or slant well, the dimensionless wellbore storage constant is sometimes expressed in terms of the effective wellbore half-length (Le / 2). In such a case, the value for wellbore radius (rw) in the above equation is replaced by the effective wellbore half-length which makes the dimensionless wellbore storage constant a very small number.
Wellbore storage is normally assumed to be constant during a test and, in practice, this assumption is often reasonable. However, there are numerous situations where wellbore storage is not constant. This changing wellbore storage may be caused by a changing wellbore fluid compressibility, by phase redistribution, or by a change in the type of storage from a changing liquid level to a liquid filled wellbore. Changing wellbore storage is accounted for using a modified form of the dimensionless wellbore storage definition, which includes additional dimensionless parameters: apparent dimensionless storage (CaD) and a storage pressure parameter (CpD).
The wellbore storage constant and dimensionless wellbore storage constant are calculated from the early time data, by performing an afterflow or wellbore storage analysis.