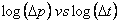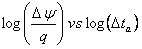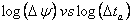Bilinear Fracture Flow Analysis
Subtopics:
Summary of Equations for Bilinear Fracture Flow
Summary of Equations for Bilinear Fracture Flow Derivative Analysis
Bilinear fracture flow is one of the flow regimes that can be identified when a reservoir has a finite conductivity vertical fracture. The purpose of analyzing bilinear fracture flow data is to determine the fracture flow capacity (kfwf).
Constant Rate Solution
For oil and water:
For gas:
Bilinear fracture flow data forms a straight line when placed on a semi-log plot of pressure versus a quad root time function (p vs. (time function)0.25) for a buildup as shown below.
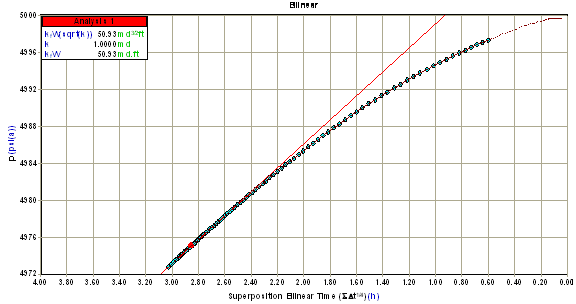
The slope (m) of this line is used to calculate root fracture flow capacity (sqrt(kfwf)) as follows:
For oil and water:
For gas:
The table below summarizes the equations used to calculate root fracture flow capacity (sqrt(kfwf)) for different fluid types and flow periods.
Summary of Equations for Bilinear Fracture Flow (Field Units)
|
|
Flow Period |
Root Fracture Flow Capacity |
|
Oil |
Drawdown
|
|
|
Buildup
|
|
|
|
Gas |
Drawdown
|
|
|
Buildup
|
|
Derivative Analysis
The signature of Bilinear fracture flow data on a derivative plot is a straight line with a slope of 1/4. The position of this line is used to calculate root fracture flow capacity (sqrt(kfwf)). Note that root fracture flow capacity increases as the position of this line moves to the right.
Starting with the constant rate solution (see above), the derivative with respect to the logarithm of quad-root time is:
For oil and water:
For gas:
Taking the logarithm of both sides:
For oil and water:
For gas:
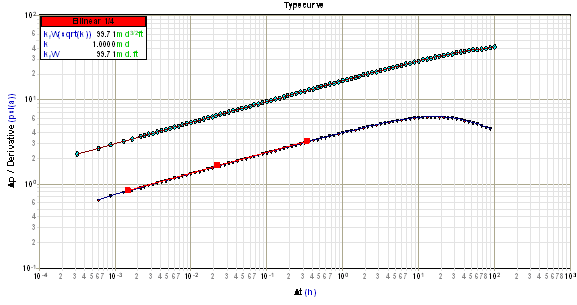
Using any derivative point on this line, the root fracture flow capacity (sqrt(kfwf)) can be determined as follows:
For oil and water:
For gas:
Summary of Equations for Bilinear Fracture Flow Derivative Analysis (Field Units)
| Flow Period | Root Fracture Flow Capacity ((md ft)0.5) |
Oil | Drawdown
| |
Buildup
| ||
Gas | Drawdown
| |
Buildup
|